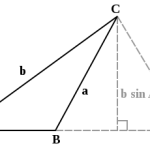
Trong hình học tam giác, định lý cosin là một trong những định lý quan trọng nhất. Định lý này cho phép chúng ta tính toán một cạnh của tam giác khi biết hai cạnh còn lại và góc xen giữa chúng.
Nội dung
Định lý cosin
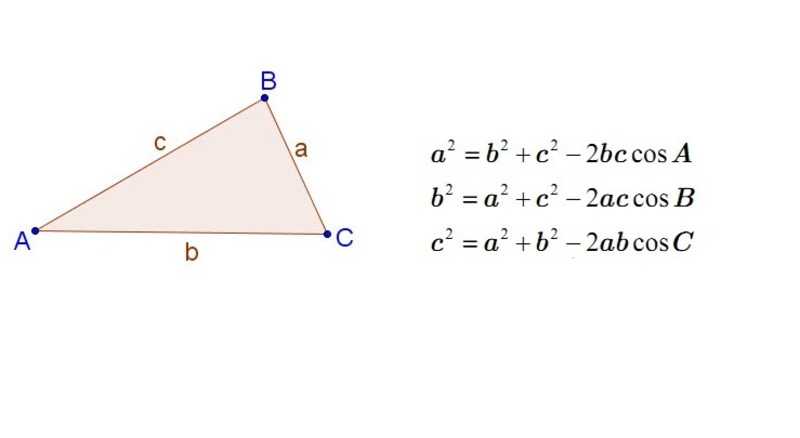
Định lý cosin được phát biểu như sau: Trong một tam giác bất kỳ, bình phương một cạnh bằng tổng bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen ở giữa chúng.
Hệ quả của định lý hàm cosin

Hệ quả định lý hàm cosin là những định lý được suy ra từ định lý hàm cosin. Chúng có thể được sử dụng để giải các bài toán tam giác một cách nhanh chóng và dễ dàng.
Một số hệ quả của định lý hàm cosin được diễn giải bằng lời, như sau:
- Cosin của một góc trong tam giác bất kì bằng tỷ số bình phương của cạnh đối diện với góc đó chia cho tổng bình phương của hai cạnh còn lại.
- Bình phương của một cạnh trong tam giác bất kì bằng tổng bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc đối diện với cạnh đó.
- Nếu biết độ dài của ba cạnh của một tam giác, ta có thể tính được số đo của các góc trong tam giác đó.
- Nếu biết độ dài của hai cạnh và góc xen giữa chúng, ta có thể tính được độ dài cạnh còn lại của tam giác đó.
- Nếu biết độ dài của một cạnh và góc đối diện với cạnh đó, ta có thể tính được độ dài của hai cạnh còn lại của tam giác đó.
Để sử dụng hệ quả định lý hàm cosin, ta cần nắm vững định lý hàm cosin và các hệ quả của định lý này. Sau đó, ta cần xác định xem hệ quả nào phù hợp với bài toán cần giải.
Ứng dụng của định lý cosin

Định lý cosin là một trong những công cụ quan trọng trong toán học và hình học, được sử dụng để giải quyết các vấn đề liên quan đến tam giác và góc vuông. Định lý cosin cho phép chúng ta tính toán các độ dài cạnh hoặc góc trong tam giác và có nhiều ứng dụng thực tế quan trọng. Dưới đây là một số ứng dụng phổ biến của định lý cosin:
- Tính độ dài cạnh tam giác: Định lý cosin cho phép chúng ta tính toán độ dài của một cạnh của tam giác khi biết các độ dài của hai cạnh khác và góc giữa chúng. Điều này rất hữu ích trong hình học và các vấn đề liên quan đến đo đạc.
- Tính toán các góc trong tam giác: Định lý cosin cũng cho phép chúng ta tính toán các góc trong tam giác khi biết độ dài của ba cạnh. Điều này có thể hữu ích trong việc xác định hình dạng và hướng của tam giác.
- Xác định tích vô hướng: Định lý cosin cũng được sử dụng trong việc tính toán tích vô hướng của hai vectơ trong không gian Euclid. Điều này có ứng dụng rộng rãi trong đại số tuyến tính và trong các lĩnh vực như vật lý và công nghệ.
- Giải quyết các vấn đề vận động: Trong vật lý và kỹ thuật, định lý cosin được sử dụng để giải quyết các vấn đề liên quan đến chuyển động và lực tác động lên các đối tượng. Nó giúp tính toán các thành phần của lực hoặc vận tốc trong các hướng khác nhau.
- Ứng dụng trong thiết kế và xây dựng: Định lý cosin cũng được sử dụng trong các ứng dụng thiết kế và xây dựng, chẳng hạn như xác định các lực căng trong các cấu trúc như cầu, tòa nhà, và thiết bị kỹ thuật.
- Xác định khoảng cách giữa các điểm: Định lý cosin có thể được sử dụng để tính khoảng cách giữa các điểm trong không gian dựa trên tọa độ của chúng.
Tóm lại, định lý cosin là một công cụ quan trọng trong toán học và khoa học, có nhiều ứng dụng thực tế quan trọng trong nhiều lĩnh vực khác nhau.
Lưu ý khi áp dụng định lý cosin trong toán học
Khi áp dụng định lý cosin trong toán học, cần lưu ý một số điểm quan trọng để đảm bảo tính chính xác và hiểu rõ về cách sử dụng công thức, dưới đây là những lưu ý quan trọng:
- Xác định cụ thể bài toán: Trước khi sử dụng định lý cosin, bạn cần xác định rõ bài toán và xem xét xem liệu định lý này có phù hợp không. Điều này bao gồm việc xác định tam giác cần tính toán và biết rõ thông tin về các cạnh và góc của tam giác đó.
- Xác định công thức cần sử dụng: Định lý cosin có hai biến thể chính – một cho tính độ dài cạnh và một cho tính toán các góc. Bạn cần xác định rõ công thức cụ thể cần áp dụng dựa trên mục tiêu của bạn.
- Biết cách tính cosin của một góc: Để áp dụng định lý cosin, bạn cần biết cách tính cosin của một góc. Trong trường hợp thông thường, bạn sẽ cần sử dụng máy tính hoặc bảng cosin để tìm giá trị cosin của góc cần tính.
- Lưu ý đơn vị: Khi tính toán, đảm bảo rằng các đơn vị của các độ dài cạnh phải là cùng một. Nếu không, bạn cần chuyển đổi chúng để có thể sử dụng định lý cosin.
- Xác định góc giữa các cạnh: Trong định lý cosin, bạn cần biết góc giữa các cạnh cần tính toán. Điều này có thể đòi hỏi bạn phải biết cách xác định góc hoặc sử dụng công thức góc trong tam giác.
- Xem xét sự hạn chế của định lý cosin: Định lý cosin không thể áp dụng cho tất cả các loại tam giác. Nó chỉ áp dụng cho các tam giác thường, không đề cập đến tam giác vuông. Đối với tam giác vuông, bạn nên sử dụng định lý Pythagoras.
Kết luận
Định lý cosin là một công thức đơn giản nhưng vô cùng hữu ích. Chỉ cần nắm vững định lý này, bạn có thể tính diện tích tam giác nhanh chóng và chính xác. Hãy áp dụng định lý cosin để giải quyết những bài toán về tam giác nhé!